Эффект бабочки
Это была темная и штормовая ночь. Грозовые тучи разрастались, сильные ливни сменялись мощными порывами ветра. Дождь лил стремительным потоком, на земле образовались струящиеся ручейки воды. На рассвете бледные лучи нового дня пробирались сквозь холодный воздух, и вода начала просачиваться в почву и испаряться.
Компьютерная метеорологическая модель Эдварда Лоренца стала предметом повышенного внимания. После завершения работы над ней в 1960 году он проводил много времени в своей лаборатории в Массачусетском Технологическом институте, исследуя климатические модели. Принцип модели Лоренца на самом деле был очень прост: основываясь на вводимых снимках погодной картины, компьютер мог дать прогноз на небольшой период времени. Данные этого расчета становились основой для последующих вычислений и так далее.
Компьютерная цепь вычислений могла воспроизводить 24 часа в минуту, после чего экран компьютера Лоренца становился сценой для драмы будущих событий: высокое давление, сменяющееся низким давлением, ураганы, вслед за которыми дул нежный ветерок, темные и штормовые ночи, после которых наступают ленивые летние дни.
Модель Лоренца была больше, чем просто будоражащей. У нее был огромный потенциал. Что если однажды станет возможным предсказывать погоду на несколько месяцев вперед?
Однако в тот зимний день 1961 года Лоренц сделал очень необычное и странное открытие. Он решил проверить предыдущее воспроизведение, на этот раз с более длинной последовательностью. Но вместо того, чтобы произвести все вычисления с начала, он попытался сократить процесс. Он ввел значения, полученные в прошлый раз, но начиная с середины цепочки. Затем он включил машину и вышел в коридор сделать себе чашечку кофе. В тот момент он совершенно не подозревал, что тем временем компьютерные итерации вели себя действительно очень странно.
Когда Лоренц вернулся, он очень удивился. Вычисления компьютера, которые должны были быть идентичны с предыдущей последовательностью, вообще выглядели неправильно. Они отклонялись все больше и больше и на два месяца вперед потеряли всякое сходство с первым воспроизведением.
Сначала он приписал это ошибке компьютера, но вскоре он понял настоящую причину. Его отправные точки цепи вычислений имели трехдесятичную точность. Однако компьютерные расчеты велись с шестью десятичными знаками, что доказывало их существенную значимость. Его собственная интуиция подсказывала, что было бы разумным не придавать значения последним трем десятичным во вводимых данных, так как едва ли их могли зарегистрировать метеорологические измерительные инструменты: насколько важна была 1/1000 или еще меньше? Но в метеорологической компьютерной модели Лоренца эти десятичные дроби доказали свою огромную значимость.
Открытие Лоренца не стало чем-то особенным для метеорологических прогнозов. Оно указало, в основном, на математический феномен, который ученые прежде никогда не замечали. Его сразу назвали "эффектом бабочки", так как реалистические имитации показали, что сложные вычисления системы сильно зависят от начальных значений, причем настолько сильно, что взмах крыла бабочки в Бразилии мог бы стать причиной возникновения торнадо в Техасе (Лоренц, 1979 год).
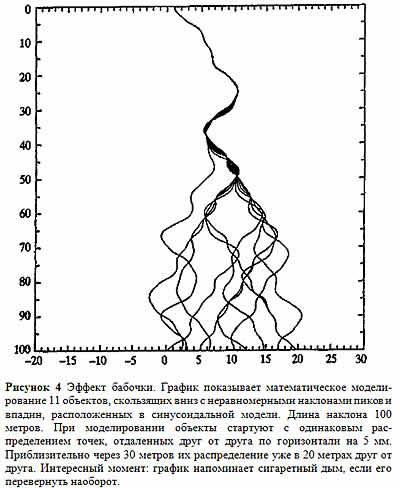 Или, говоря финансовым языком: маленькая старушка, продающая несколько облигаций в Брюсселе, могла бы стать причиной краха в Японии! И выяснилось, что эта зависимость касалась не только сложных моделей: эффект бабочки можно было также обнаружить и в простых нелинейных моделях, демонстрирующих неустойчивость.
Или, говоря финансовым языком: маленькая старушка, продающая несколько облигаций в Брюсселе, могла бы стать причиной краха в Японии! И выяснилось, что эта зависимость касалась не только сложных моделей: эффект бабочки можно было также обнаружить и в простых нелинейных моделях, демонстрирующих неустойчивость.
Последствия этого открытия были революционными. Представьте себе, что поверхность Земли покрыта сетью метеостанций с трехдесятичной точностью, находящихся только в 30 см друг от друга, посылающих свои измерения в центральный компьютер каждую минуту. И предположите, что этот компьютер достаточно большой, чтобы вместить в себя совершенно правильную модель глобальных погодных моделей.
Если бы даже и было так, то надежный прогноз погоды на месяц вперед сделать просто невозможно. Как раз вопреки своим первоначальным намерениям и ко всеобщему удивлению, Лоренц смог доказать, что невозможно и никогда не будет возможно давать долгосрочные прогнозы погоды.
Эффект бабочки — один из элементов системы математических феноменов, с тех пор обобщенно названных термином "детерминированный хаос". Этот феномен охарактеризован Чера Л. Сайерсом следующим образом (1989): "Процесс характеризуется детерминированным хаосом, если он генерирован полностью детерминированной системой1, возникающей как результат беспорядочно функционирующих рядов в стандартных временных диапазонах".
Нас окружает хаос. Представим себе дымок сигареты в тихой комнате. Тысячи микроскопических частиц дыма поднимаются узкой колонкой, подталкиваемые горячим воздушным потоком. Затем внезапно колонка прерывается, заменившись турбулентными, постоянно меняющимися завихрениями дыма. Линейный поток трансформировался в хаос. И это происходит независимо от того, где вы находитесь. Или рассмотрим игру в футбол. Ни один, даже самый проницательный эксперт не сможет предугадать, где мяч окажется всего лишь через 10 секунд.
Хаос наступает главным образом в отношениях, где присутствуют самопроизвольные усиливающиеся механизмы. Вообразите себе систему, в которой событие "А" приводит к событию "В", а событие "В" к событию "С". Если событие "С" затем воспроизводит событие "А", тогда в этом процессе есть простая цепь положительной обратной связи.
Если мы попытаемся наметить в общих чертах взаимоотношения в экономике страны, как если бы это была метеорология, то вскоре столкнемся со сложными вариантами этих механизмов. Среди хорошо известных примеров есть так называемые эффекты мультипликации и акселерации, тезаврирование, самопроизвольное усиление ожиданий роста ("держаться наравне с Джонесесом"), увеличение потребностей в капитале из-за смещений во взаимоотношениях труда и капитала и т. д., — все вместе эти многочисленные цепочки обратных связей могут означать, что системы имеют не просто равновесие, а сами себя раскачивают или демонстрируют иные сложные движения.
Каждая из этих положительно воздействующих цепей обратных связей может вносить свой вклад в самопроизвольно усиливающую природу экономического феномена, пока окончательно не будет заторможена другими механизмами. Чтобы правильно описать эти системы, необходимо применить нелинейную математику.
- Поиски индивидуальности: тревоги, деньги
- Почему мастер сказал «игра»?
- Любимые книги мистера Джонсона
- Тип личности, способной делать деньги
- Действительно ли биржа это толпа?
- Хотите сказать, что деньги и есть это самое?
- Прижимая к груди «Комсат»
- Я хочу, чтобы меня любили за меня самого
- Ну и дурак же я был!
- IBM как религия: Не трогать, не трогать!
- Брокер или шаман
- А можно, я скажу Розалинде?
- Из-за них у меня все идет наперекосяк
- Тревоги и поиски индивидуальности
- Где деньги лежат
- Мистер Смит признается в своей предвзятости
- Системы:
- Они: профессионалы
- Может ли все это рухнуть?
- Жадность и страх
- Четыре ужасные правды о финансах
- Барометр Бебсона
- Отрицательная производная первой степени
- Небольшой эксперемент
- Крах в Голландии в 1636 году
- Пузырь красного моря
- Биржевой крах 1929 года
- Эффект бабочки
- Тайна Роберта Мэя
- Самомоделируемые системы
- Экономический и финансовый хаос
- Графики являются самореализующимися
- Кейнс и конкурс красоты
- Древо знаний
- Психология рыночной информации
- Психология трендовых рынков
- Конец света
- Позиции и изменения позиций
- Психологические явления во время паники
- Вторичные эмоции и паника
- Когда продолжение становится решающим
- Неоправданные ожидания и тройной шок
- Скользящая средняя
- Репрезетативность и тренды
- Линии тренда, каналы и музыкальные стулья
- Подтверждения объемов
- Чрезмерная самоуверенность
- Затаив дыхание и передумывая
- Флаги и вымпелы: взятие прибыли
- Гэпы: вакуум покупателей или продавцов
- Треугольники: неопределенность
- Гармония и резонанс
- Индикаторы
- Товары
- Перекупленные и перепроданные рынки
- Психология решающих моментов
Психология финансов